[딥러닝] 6. 엔트로피 (Entropy)
목차
1. 엔트로피의 정의
2. 엔트로피가 왜 중요한가?
2-1. Entropy measures the uncertainty.
2-2. The reduction of entropies measures the amount of information.
2-3. Entropy is the fundamental limit for the compression of information.
2-4. Entropy measures how far two probability distributions are to each other. This plays a key role in Machine Learning
3. 내용 정리전 장 손실함수(loss function)에서 다뤘던 내용 중, 손실함수 중 MSE , CEE는 둘 다 공간 상에서의 두 좌표의 거리를 이용한다는 내용을 다뤘습니다. 사실 앞으로 MSE 보다 CEE를 더 많이 사용합니다.
대체, log와 공간상에서 두 점 사이의 거리가 어떤 상관관계를 가지는지? 에 대해 알아보겠습니다.
1. 엔트로피의 정의

p(x)는 확률 변수로 가정했을 때, 확률 변수에 대하여 엔트로피 h(x)는 다음과 같이 정의됩니다.
H(x) = -∑p(x)log(p(x)) , 이때 log의 밑은 2입니다. 추가적으로 0*log0 = 0입니다.
고등수학에서 다뤘던 로그의 밑은 대부분 자연수 10 이거나, 자연상수 e 였습니다.
하지만, 컴퓨터를 다루는 정보이론에서는 2진법에 의해 지수의 밑을 2로 하게 됩니다.
그나저나, 0log0이 어떻게 0인거죠? 라고 궁금하실 겁니다. 맞습니다. 원래 0log0은 불능입니다.
xlogx를 x->0에서의 극한값을 취했을 때, x를 1/t로 치환을 하고 분모분자 로피탈을 구해주면 0이 나오게 됩니다.
정보이론에서는 확률변수 중 0도 있을 수 있으니, 0log0을 0이라 보자 약속을 한 것입니다.

한 가지 예시를 들겠습니다.
어떤 사람이 서로 다른 카드를 여러 장 (a, b, c, d) 카드를 들고 있는데, 그때의 각 카드를 집을 확률이 (1/2, 1/4, 1/8, 1/8)이라고 해보겠습니다.
이때, 확률 변수 X에 대한 엔트로피는 공식에 의해서 위 식처럼 나오게 됩니다. 7/4 bits 가 나왔죠.
다음은 스무고개 게임입니다.

어릴 때, 스무고개 게임 많이들 해보셨을 겁니다.
a카드를 집을 확률이 1/2로 절반이니까 당연히 질문을 최소화하는 방법에 효과적인 질문은 '카드가 a입니까?' 가 되겠죠.
그다음 효과적인 질문은 b, 그리고 c, d or (d, c)가 될 것입니다. 왜냐하면 확률이 1/2,1/4,1/8,1/8이었으니까요.
이때, 질문개수의 기댓값을 구해볼 수 있습니다.

분수들은 해당 카드의 확률이고, 자연수는 누적질문 개수입니다.
1/8 x 3 x 2 에서 2를 곱한 이유는 c, d / d, c의 경우 결과가 동일하기 때문입니다.
바로 위에서 구했던 엔트로피 결과값이랑 7/4로 동일하죠? 사실, 이것이 우연의 일치가 아닙니다.
계속해서 보겠습니다.
다음은

8마리의 말이 참가하는 경마가 있다고 가정해 봅시다. 여덟 마리의 말이 우승할 확률이 (1/2,1/4,1/8,1/64,1/64,1/64,1/64(라고 가정했을 때, 경마의 엔트로피는 2 bits 가 나오게 됩니다.
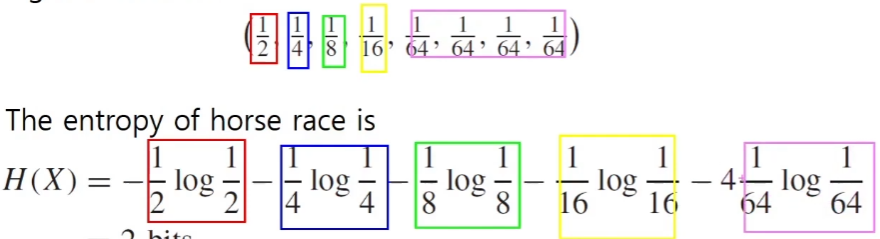
2. 엔트로피가 왜 중요한가?
1) Entropy measures the uncertainty.
엔트로피는 불확실성을 측정합니다. 현대과학의 특징이 어떤 대상을 측정하고 계량화까지 하는데 심지어 어떤 것까지 계량화를 하냐면 불순도까지 계량화를 합니다.
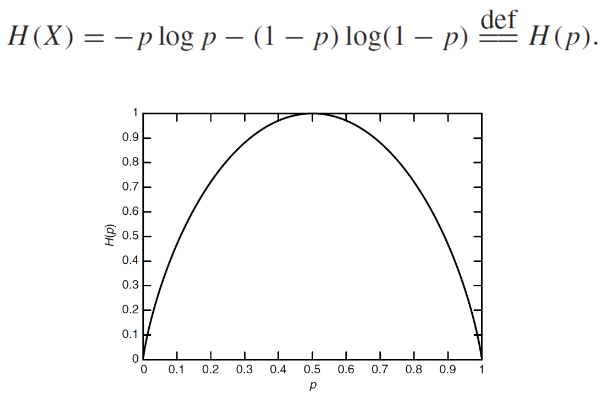
entropy formula에 대한 graph입니다. 동전 던지기 같은 경우 p와 1-p가 1/2일 때, 엔트로피는 1이었죠?
그러면, 동전 던지기를 할 때, 앞면이 어떤 확률로 나와야 불확실성이 제일 클까요? 당연히 1/2입니다.
1이거나 0 인경우 앞면이 정확하게 나오거나 아예 안 나온다는 것인데, 이때는 불확실성이 없고 확실성이죠.

좀 더 일반화한 것입니다. 엔트로피 H(X)는 log|χ|를 못 넘습니다. χ는 확률 변수를 취하는 값의 개수입니다.
근데 H(X)와 log|χ| 가 언제 같아지냐면, 확률변수가 균등분포를 취할 때 같아집니다.
동전 던지기 경우, H(X) = 2 , |χ| 는 1/2,1/2 총 2개, log|χ| =2 >>>>> H(X) = log|χ|
주사위 경우, H(X)는 log6을 넘지 못하고 또, 균등분포를 취할 때는 같아집니다.

조건부 엔트로피는 위 그림처럼 정의됩니다. 사실, -log p(y|x) 의 기댓값을 구하는 것으로 해석할 수 있습니다.

예시를 들겠습니다.
X에 대한 marginal distribution은 그림처럼 열 별로 더했을 때 값들이고,
Y에 대한 marginal distribution은 반대로 행 별로 더했을 때 값들입니다.

이때, H(X|Y) 를 구하면 11/8 bits가 나오고. H(Y|X) 는 13/8이 나오게 됩니다. 둘이 꼭 같을 필요는 없습니다.

H(X|Y) 값 역시 H(X)를 넘지 못합니다. 개념적으로 보지 말고 그냥 상식적으로 생각해 보죠.
어떤 확률 변수 X가 있는데, 그 값에 대해 조건 Y를 가정하면, 당연히 그 불확실성은 가정하지 않은 것보다 더 줄어들겠죠? 그 뜻입니다.
다만, 확률 변수 X 와 Y가 독립일 경우에는 불확실성에 영향을 받지 않을 겁니다.
결론, 조건부 엔트로피는 <= 엔트로피

condtitional entropy가 0이라는 것은 결정론적인 상황이리는 것입니다. 즉, Y가 X로 함수 표현이 가능하는 것입니다.
2) The reduction of entropies measures the amount of information.
엔트로피의 감소는 정보의 양을 측정합니다. 정보의 양을 수학적으로 나타내는 것이 생각보다 쉽지 않을 일입니다.
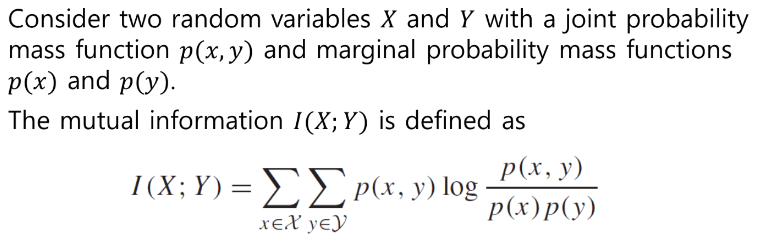
x, y 둘 사이의 상호 정보량을 위 그림처럼 정의합니다. log(p(x, y)/p(x) p(y)) 의 기댓값으로 정의를 하는 것이죠.
위 공식을 전개하여 풀어서 쓰면 다음과 같은 결론이 도출됩니다.

H(X) - H(X|Y) 인 이유는 아까도 말씀드렸다시피, H(X|Y)는 Y를 알았을 때의 X의 엔트로피였습니다.
그리고 H(X|Y)는 H(X) 보다 작을 수밖에 없었습니다. 근데 이 두 개를 빼면 불확실성이 얼마나 줄어들었는지 알 수 있습니다. 즉, 정보의 양이 나온다는 것입니다.
간단한 예시를 보겠습니다.

아까 다 구했던 값들입니다. 두 개를 빼면 3/8입니다.
해석을 하면 원래의 x의 불확실성은 7/4였고, y를 알게 됨으로써 불확실성이 11/8로 내려갔습니다.
즉, 두 개의 차인 3/8 만큼 정보의 양이 측정이 된 것입니다.
정보의 양을 측정하는 것이다 보니 당연히 딸려 나오는 성질인데요

정보의 양이 음수일 수는 없죠. 정보의 양이 0이라는 의미는 x와 y가 서로 영향을 받지 않는 독립인 상태입니다.
3) Entropy is the fundamental limit for the compression of information.
정보를 압축함에 있어서 한계지점이 발생하기 마련인데, 그 한계 지점이 엔트로피일 때입니다.
한 가지 예시를 보겠습니다.
코드 길이의 기댓값을 생각해 보면,확률 질량 함수 p(x)를 갖는 랜덤 변수 X에 대한 코드 C(x)의 예상 길이 L(C)는 다음과 같습니다.
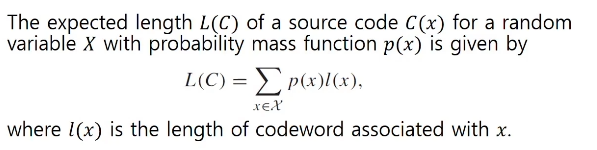
그래서 효율적으로 코드를 보낸다는 것은 기댓값을 낮춘다는 것입니다.

아까 했던 스무고개 예시에 카드에서 코드로만 바뀐 것입니다. codeword도 추가됐습니다.
코드의 기댓값은 마찬가지로 7/4입니다.

shannon의 정리입니다. 단어를 코드를 바꿔서 보낼 때 가급적이면 압축해서 작은 데이터로 보내는 것이 좋은데, 압축할 때에는 한계가 발생합니다. 그 한계지점이 바로 엔트로피라는 것입니다.
optimal code라는 것은 최적의 코드입니다.
그 코드는 이론적으로 엔트로피와 엔트로피 +1 사이에 두면 최적의 한계지점에서 압축을 해서 작은 데이터를 보낼 수 있습니다.
4) (Relative) Entropy measures how far two probability distributions are to each other.
This plays a key role in Machine Learning
(상대) 엔트로피는 두 확률 분포가 서로 얼마나 멀리 떨어져 있는지 측정합니다. 이것은 기계 학습에서 핵심적인 역할을 합니다.
relative entropy의 정의는 다음과 같습니다.
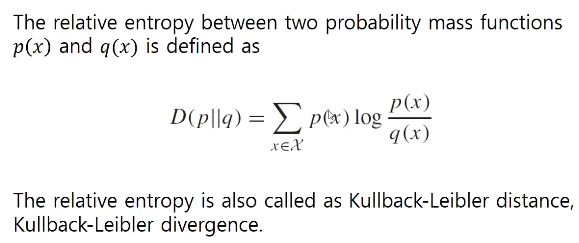
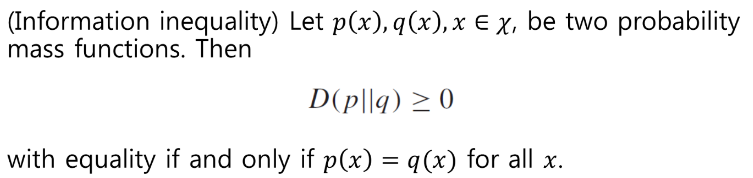
두 확률변수의 거리를 구하는 것이기 때문에, 당연히 음수가 될 수 없습니다. 거리가 0이 될 필요충분조건은 두 확률 변수가 같다는 것이죠.
상호 정보의 엔트로피 일반화 공식입니다.
I(X;X) = H(X)인 이유는 X라는 것을 알고 있을 때 불확실성이 없으니 본인 엔트로피가 나옵니다.
이걸 Self Information 이라 부르기도 합니다.
또, Relative entropy는 Mutual information을 일반화하는데, 확률분포를 아래와 같이 넣습니다.
두 확률분포 사이(파랑, 빨강)에 얼마나 가깝냐 머냐 Relative entropy를 구하는 것이, 곧 Mutual information이 됩니다.

3. 내용 정리
전 포스팅에서 다뤘던 CEE의 공식입니다.
아래는 Relative entropy와 Cross entropy의 관계입니다.
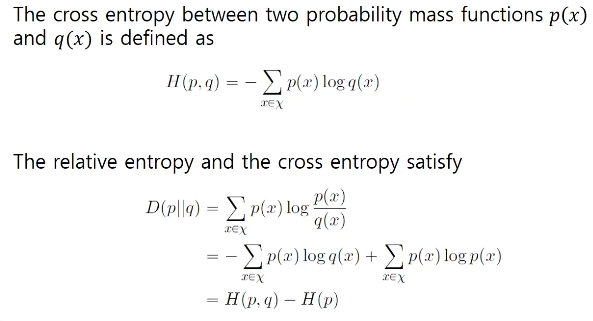
머신러닝에서 학습을 시킬 때는 보통 p를 고정을 시키고 합니다.
다시 말해, H(p)는 상수가 되고, q를 얼마나 q에 근사 시키는가에 따라 학습의 성능이 좌지우지되는 셈이죠.
그래서, Relative entropy(D(p||q))를 줄인다는 말은 H(p, q)를 줄인다와 같은 말이 됩니다.
여태 다뤘던 얘기들을 모두 모아 다시 보겠습니다.

마지막 정리하겠습니다. 학습을 할 때에 성능이 좋다는 말은 빨간 테두리와 파란 테두리의 점 사이의 거리가 가깝다는 것이 되고, 성능이 안 좋다는 말은 거리가 멀다는 말이 됩니다.
-log(yk)가 도출되는 이유는 계속 강조했듯이, one-hot 확률벡터는 본인을 제외하고 나머지가 다 0이 되기 때문에, 불확실성이 없다는 말과 같습니다. 그렇기 때문에 0이 곱해지는 나머지 식들은 다 제거하고 남은 것이 -log(yk)가 되는 것이죠.
참고 문헌
[1] 참고 영상