목차
1. 퍼셉트론(Perceptron)이란?
2. 뉴런의 구조
3. 게이트
3-1. AND 게이트
3-2. NADN 게이트
3-3. OR 게이트
3-4. XOR 게이트
3-5. 기하학적 게이트
4. 퍼셉트론의 종류
4-1. 단층 퍼셉트론
4-2. 다층 퍼셉트론
4-3. XOR 게이트 한계 극복
5. Python으로 게이트 구현1. 퍼셉트론(Perceptron)이란?
퍼셉트론(Perceptron)이란 인공신경망(Artificial Neural Network, ANN)의 구성요소(unit)로서 다수의 값을 입력받아 하나의 값으로 출력하는 알고리즘입니다.
Perceptron = Perception + Neuron 이며 인공 뉴런이라고도 합니다.
생물학에서 다루는 신경계(Neural Network)의 기본 단위인 '뉴런'의 동작 과정을 통계학적으로 모델링한 알고리즘입니다.

그림1을 보시게 되면 x1, x2가 입력값으로 들어가게 되고 가중치(weight)를 만나 x1*w1 + x2*w2 ==> y 가 됩니다.
정해놓은 임계값(𝜽)에 비교해 y가 𝜽보디 작거나 같으면 0, y가 𝜽보다 크면 1로 분류합니다. 왜냐하면 컴퓨터는 이진분류이니까요. 컴퓨터에 입력하기 전에 알아들을 수 있게 바꿔주는 겁니다.
이 구조를 뉴런의 구조와 비교해 볼까요?
2. 뉴런의 구조
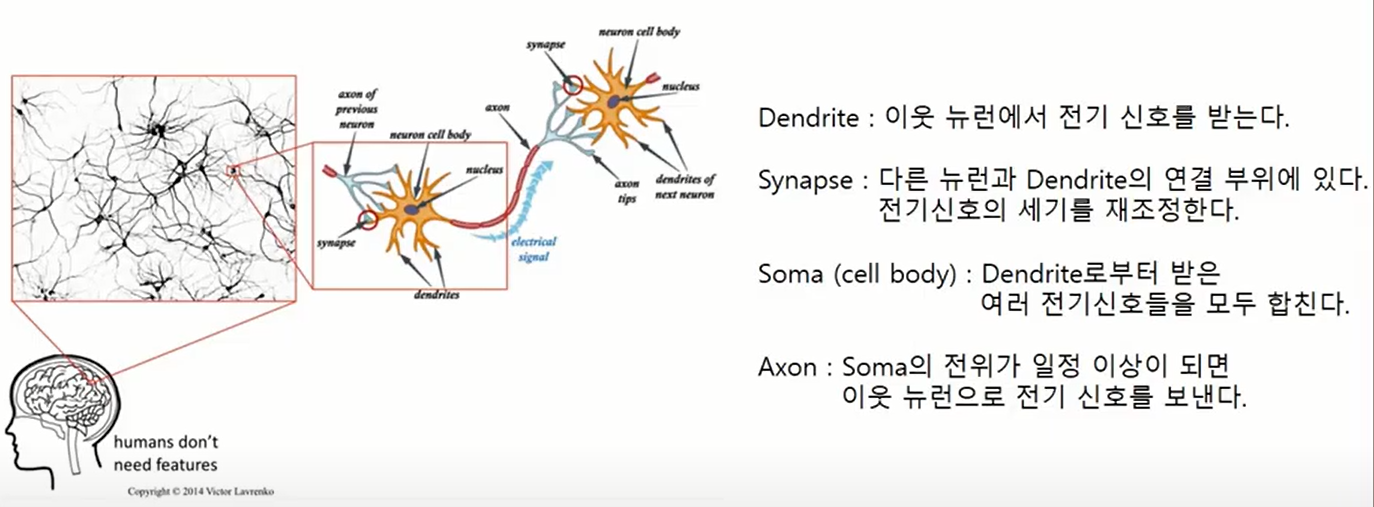
Dendrite가 이웃 뉴런에서 전기신호를 받고, Synapse에서 전기신호 세기를 조절하고 Soma에서 모두 모았다가, 일정 임계치 이상이 되면 Axon을 통해 이웃 뉴런으로 전기 신호를 보냅니다.
마치 퍼셉트론 구조와 흡사하죠?
자 다시, x1 x2가 입력값으로 들어오고, 가중치 w1 w2를 만나 x1*w1 x2*w2가 되고, 모두 모아 x1*w1 + x2*w2 = y가 되고, y가 일정 임계치 𝜽보다 크면 신호를 보낸다(1) / y가 일정 임계치 𝜽보다 작으면 신호를 보내지 않는다(0)
이 뉴런의 구조를 봉화 시스템으로 예를 들어볼게요.
교통이 불편했던 옛날에는 급한 소식을 전할 때, 불을 피워서 불빛이나 그 연기로 신호를 보냈었죠.
그 중에서 봉화는 가장 빨리 소식을 전달할 수 있는 방법이었습니다. 봉화는 불빛과 연기로써 소식을 전하는 것인데요,
1번 봉화에서 불을 피우고, 2번에서는 1번봉화를 보고 불을 피울지 말지 정하는데, 만약 안개 때문에 1번봉화가 보이지 않으면 2번 봉화에서는 그 불이 잘 식별이 안되죠. 반대로 안개 없이 잘 보이면, 2번 봉화에서는 불을 피우는 것이죠.
이런식으로, 뉴런과 퍼셉트론은 출력층에서 일정 임계치가 되면 신호는 보내는 것입니다.
3. 게이트
임계치 초과 = 신호를 보낸다 = True = 1
임계치 이하 = 신호를 안 보낸다 = False = 0
퍼셉트론에는 4가지 게이트가 존재합니다. (AND, NAND, OR, XOR)
여기서 우리는 3 개의 값을 정해야 합니다. 바로, w1, w2, 𝜽 입니다.
1) AND 게이트

AND 게이트 입니다. 사진을 보시다시피 T+T=T 를 제외하곤 다 False를 출력합니다.
AND 게이트를 만족시킬 수 있는 w1, w2, 𝜽 값은 어떻게 될까요? 답은 굉장히 많습니다.

w1 = 0.5, w2 = 0.5, 𝜽 = 0.7로 잡아보자!
위에서 설명 드렸다시피, 1 = True / 0 = False 입니다.
T + T 인 경우 1 이 나와 정해놓은 임계치 0.7 보다 높아 1을 반환합니다.
T + F, F+T 인 경우 0.5가 나와 0.7보다 작아 0을 반환합니다.
F + F인 경우 0이 나와 0.7보다 작아 당연히 0을 반환합니다.
2) NAND 게이트

NAND 게이트는 Not AND 게이트입니다. 즉, AND 게이트 출력값의 반대값을 출력하는 것이죠.

w1 =- 0.5, w2 = -0.5, 𝜽 = -0.7로 잡아보자!
NAND는 결론부터 말씀드리면, AND 게이트 에 마이너스(-) 부호를 곱해주고 부등호를 바꿔주면 됩니다.
아래 5)번에서 기하학적으로 접근하는 설명 있습니다.
T + T 인 경우 -1 이 나와 정해놓은 임계치 -0.7 보다 작아 0을 반환합니다.
T + F, F+T 인 경우 -0.5가 나와 -0.7보다 커 1을 반환합니다.
F + F인 경우 0이 나와 -0.7보다 커 0을 반환합니다.
3) OR 게이트

OR 게이트는 AND 게이트에 비해 장벽이 낮죠? 왜냐하면 충분조건이기 때문이죠. True 하나만 있어도 True가 출력되듯이
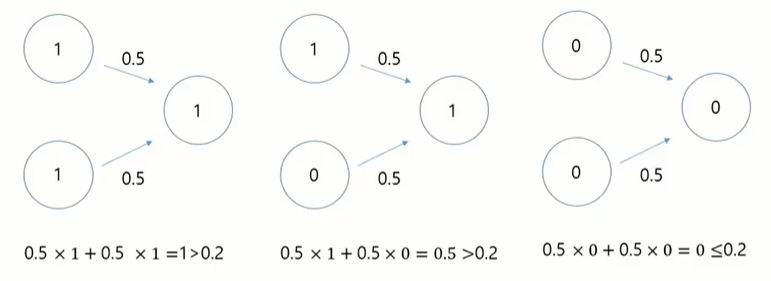
w1 = 0.5, w2 = 0.5, 𝜽 = 0.2로 잡아보자!
그렇기에, AND에서 임계치만 더 낮추면 되겠죠?? 허들이 낮아졌으니..
T + T 인 경우 1 이 나와 정해놓은 임계치 0.2 보다 커 1을 반환합니다.
T + F, F+T 인 경우 0.5가 나와 0.2보다 커 1을 반환합니다.
F + F인 경우 0이 나와 0.2보다 작아 0을 반환합니다.
4) XOR 게이트

XOR 게이트는 베타적인 논리값들을 True로 반환하는 것입니다.
표에서 볼 수 있듯이 T F = T(1) / F T = T(1)이 되는 것이죠.
XOR 게이트는 단층 퍼셉트론으로 해결할 수 없습니다. 그 이유는 좀 더 기하학적으로 접근할 필요가 있습니다.
5) 기하학적 게이트
앞서 4가지 게이트를 살펴 보았는데 게이트 개념은 좀 더 기하학적으로 접근하여 더 살펴볼 필요가 있다고 생각합니다.
아래 그림은 제가 설명을 돕기위해 직접 그린 그래프들입니다.

먼저 AND 입니다.

우리는 w1, w2, 𝜽 를 정했었습니다.
w1 * x1 + w2 * x2 = y > 𝜽 ---> 1
w1 * x1 + w2 * x2 = y <= 𝜽 ---> 0
앞서 w1 = 0.5, w2 = 0.5, 𝜽 = 0.7로 잡았습니다.
0.5*x1 + 0.5*x2 >= 0.7 이 부등식에서 우측 상수를 1로 만들어주면 x1/1.4 +x2/1.4 >= 1이 됩니다. 이 부등식은 x,y절편이 1.4이고 x1/1.4 +x2/1.4 = 1 직선을 그었을 때, 그 직선포함 위 부분을 의미하겠죠. 그렇기에 AND 게이트를 만족하는 한 직선을 그었을 때 점(1,1) 만을 만족해야하니 우측의 있는 그림의 색칠되어있는 공간 안에 있게 되겠죠.
즉, AND 게이트를 만족시킬 수 있도록 하는 w1,w2,𝜽 를 정하려면 그림의 색칠되어있는 부분에 한해서 정하면 됩니다.
1 < x1 + x2 < 2
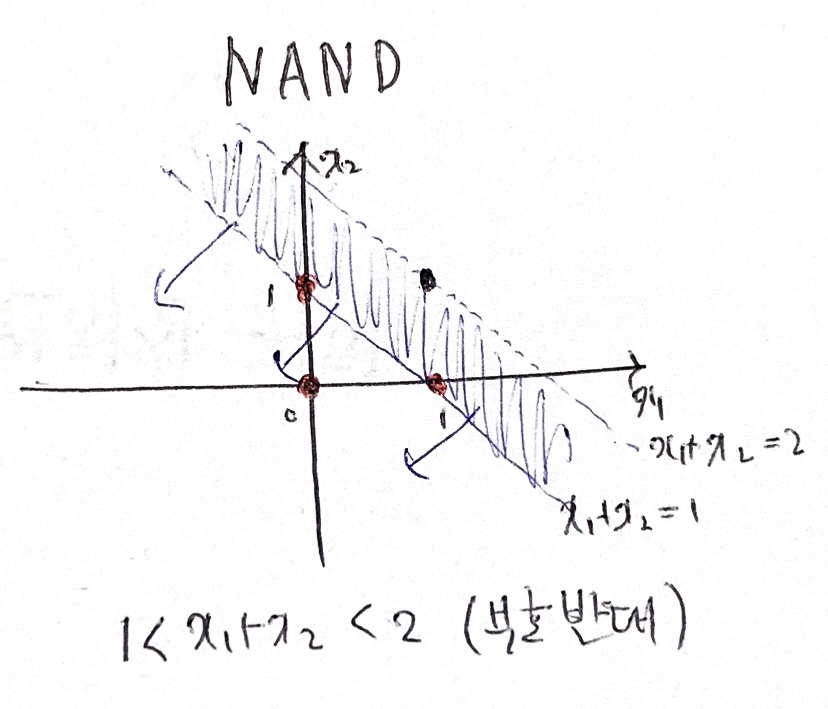
NAND 입니다.
앞서 NAND 게이트를 소개할 때 결론부터 말씀드렸었는데요,
일단 수식부터 보겠습니다.
-0.5*x1 - 0.5*x2 >= -0.7 (AND 게이트에 마이너스 곱, 부호반대)
AND 게이트에 마이너스 곱을 해주면 사실, 그 식과 AND 게이트 식은 서로 동치입니다. 근데 우리가 원하는 값은 AND 출력값에 반대를 출력해야하니 부호를 아래로 바꾼것이죠.
그래서 (1,1)을 제외한 나머지를 부등식에 만족을 시켜야하므로, 직선은 1<x1+x2<2 인셈이죠.

다음은 OR 게이트입니다.
AND 게이트에서 허들을 낮게 한 것이 OR 게이트라 했었습니다.
네 말 그대로, 임계치 𝜽를 AND보다 낮췄으니, 그래프를 그렸을 때 우측의 그림과 같이 0 < x1 + x2 < 1 을 만족하도록 그려야합니다.
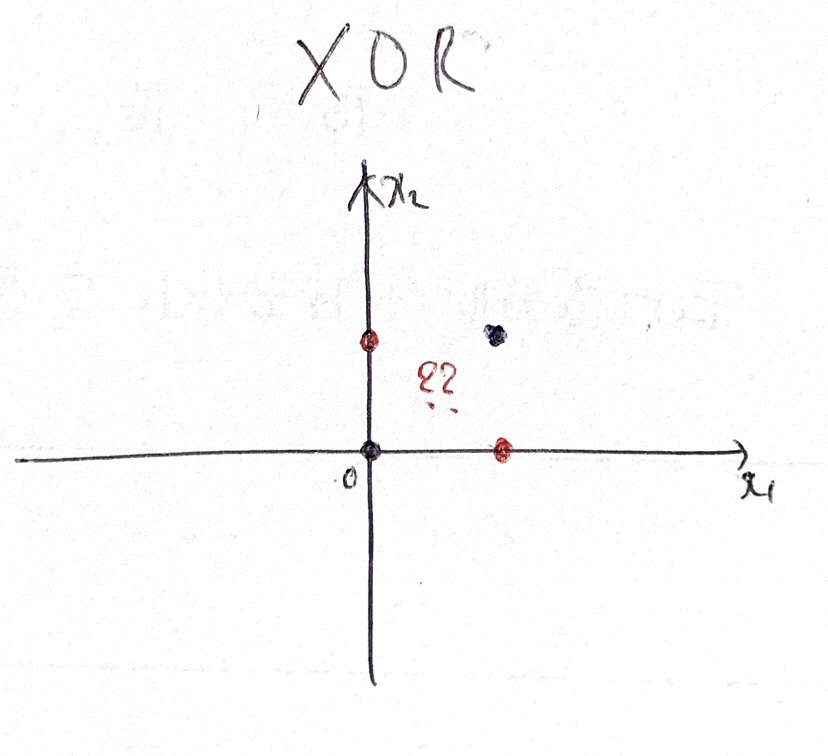
마지막 XOR 게이트 입니다.
?
??
???
????
이것은 마치 빨간점과 파란점이 좌측의 그림처럼 있는데, 두 직선이 겹치지 않도록 점들을 각각 연결해라. 라는 문제와도 같은 셈입니다.
네 그렇습니다. 사실 XOR 게이트는 위의 3가지 게이트와는 다르게 단층퍼셉트론으로는 해결하지 못합니다.
그래서 나온 것이 다층퍼셉트론입니다.
4. 퍼셉트론의 종류
퍼셉트론의 종류는 입력층(Input Layer)과 출력층(Output Layer) 사이에 은닉층(Hidden Layer)의 존재 여부에 따라 단층(Single-Layer) 퍼셉트론과 다층(Multi-Layer) 퍼셉트론으로 나뉩니다.
1) 단층퍼셉트론
단층퍼셉트론은 은닉층 없이 입력층과 출력층만 있는 경우를 단층 퍼셉트론이라 부릅니다. 단층 퍼셉트론은 디지털 논리 회로 개념에서 AND, NAND, OR 게이트를 구현할 수 있지만, XOR 게이트는 구현하지 못한다는 한계가 있습니다.
2) 다층퍼셉트론

아래 그림 과 같이 입력층과 출력층 사이에 1개 이상의 은닝층이 있는 경우를 다층 퍼셉트론(Multi-Layer Perceptron, MLP)이라 부릅니다. 다층 퍼셉트론은 단일 퍼셉트론이 XOR 게이트를 구현하지 못한다는 한계를 보완하기 위해 등장하였습니다. 다층 퍼셉트론은 AND, NAND, OR 게이트를 조합하여 XOR 게이트를 구현합니다. XOR 게이트는 은닉층 1개를 추가하여 구현할 수 있지만, 다층 퍼셉트론은 더욱 복잡한 문제를 해결하기 위해 일반적으로 2개 이상의 은닉층을 추가합니다. 이처럼 2개 이상의 은닉층을 가진 다층 퍼셉트론을 심층신경망(Deep Neural Network, DNN)이라 부릅니다. 우리가 흔히 아는 딥러닝(Deep Learning)은 이러한 심층신경망을 학습(Learning)하는 것을 의미하죠.
3) XOR 게이트 한계 극복

다층 퍼셉트론을 통한 XOR 게이트 한계 극복입니다.
위에 사진중 AND NAND OR의 모형들을 볼 수 있는데 그냥 헷갈리시면, 동그마리 안에 AND 이런식으로 표시해도 됩니다. 이 다층 퍼셉트론 모델을 통해서 베타적인 논리값들로 인한 출력값을 낼 수 있게 되었습니다.
5. Python으로 게이트 구현
AND, NAND, OR, XOR 이 4가지 게이트를 직접 Colab에서 함수를 짜보았습니다.
Perceptron Python 구현
Google Colaboratory Notebook
Run, share, and edit Python notebooks
colab.research.google.com
'딥러닝' 카테고리의 다른 글
| [딥러닝] 6. 엔트로피 (Entropy) (0) | 2023.02.05 |
|---|---|
| [딥러닝] 5. 손실 함수(Loss function) (0) | 2023.02.04 |
| [딥러닝] 4. MNIST (2) | 2023.02.02 |
| [딥러닝] 3. 인공신경망(ANN, Artificial Neural Network) (0) | 2023.02.01 |
| [딥러닝] 2. 활성화 함수 (0) | 2023.02.01 |